Tutorial: differential expression analysis on single cell RNA-seq data • countsplit.tutorials

In this tutorial, we use two simple simulated data sets to demonstrate how to use the countsplit package and base R functions (e.g. glm, kmeans) to cluster and test for differential expression in scRNA-seq data. See our [cross-validation tutorial]((https://anna-neufeld.github.io/countsplit.tutorials/articles/MSE_tutorial.html) for details on how to use the countsplit package to evaluate the output of a clustering. See the non-introductory tutorials on this website to learn how to integrate the countsplit package into three existing scRNA-seq data analysis workflows for differential expression analysis in R: Seurat, scran, and monocle3. . We start by loading the packages we will be working with. Make sure that remotes is installed by running install.packages("remotes"), then type

remotes::install_github("anna-neufeld/countsplit")

library(countsplit)
library(Matrix)
library(ggplot2)
library(patchwork)

Simulated Poisson data with no true signal.

First suppose that we have \(n=1000\) cells and \(p=200\) genes. Suppose that every count \(\textbf{X}_{ij}\) is drawn from a \(\text{Poisson}(5)\) distribution. We first generate this data.

set.seed(1)
n <- 1000
p <- 200
X <- matrix(rpois(n*p, lambda=5), nrow=n)

In this tutorial, we are interested in knowing which genes are differentially expressed across discrete cell types. We will cluster this data to estimate cell types and then test for differential expression. Since there are no true cell types and no truly differentially expressed genes in this data, a test of differential expression that controls the Type 1 error rate should give uniformly distributed p-values on this data.

The naive method

First, we will demonstrate that estimating the clusters and testing for differential expression using the same data does not control the Type 1 error rate. We refer to the practice of using the same data for clustering and differential expression testing as the “naive method” or “double dipping”.

clusters.full <- kmeans(log(X+1), centers=2)$cluster
results.naive <- t(apply(X, 2, function(u) summary(glm(u~as.factor(clusters.full), family="poisson"))$coefficients[2,]))
head(results.naive)
##         Estimate Std. Error   z value     Pr(>|z|)
## [1,]  0.03958456 0.02820810  1.403305 1.605260e-01
## [2,] -0.10237171 0.02857552 -3.582497 3.403252e-04
## [3,]  0.11308989 0.02849956  3.968127 7.243959e-05
## [4,]  0.10833419 0.02828266  3.830410 1.279301e-04
## [5,] -0.08088836 0.02823097 -2.865235 4.166997e-03
## [6,]  0.04539730 0.02797837  1.622586 1.046780e-01

The first line clusters the cells by applying k-means clustering with k=2 on the log-transformed data with a pseudocount of 1, and saves the cluster assignments as clusters.full. The second line tests for differential gene expression using Poisson GLMs. For every gene \(X_j\) in X, we fit a Poisson GLM of \(X_j\) on clusters.full, and save the summary of the slope coefficient in results.naive. As shown in the output, we have saved a slope coefficient estimate, a standard error, a z-value, and a p-value for every gene in the dataset.

Even in these first 6 rows of results, we can see that the naive method assigns small p-values to many genes, despite the fact that no genes are truly differentially expressed in this data. We can make a uniform QQ-plot of the p-values for the naive method to see that they are not uniformly distributed and thus do not control the Type 1 error.

ggplot(data=NULL, aes(sample=results.naive[,4]))+geom_qq(distribution=stats::qunif)+geom_abline(col="red")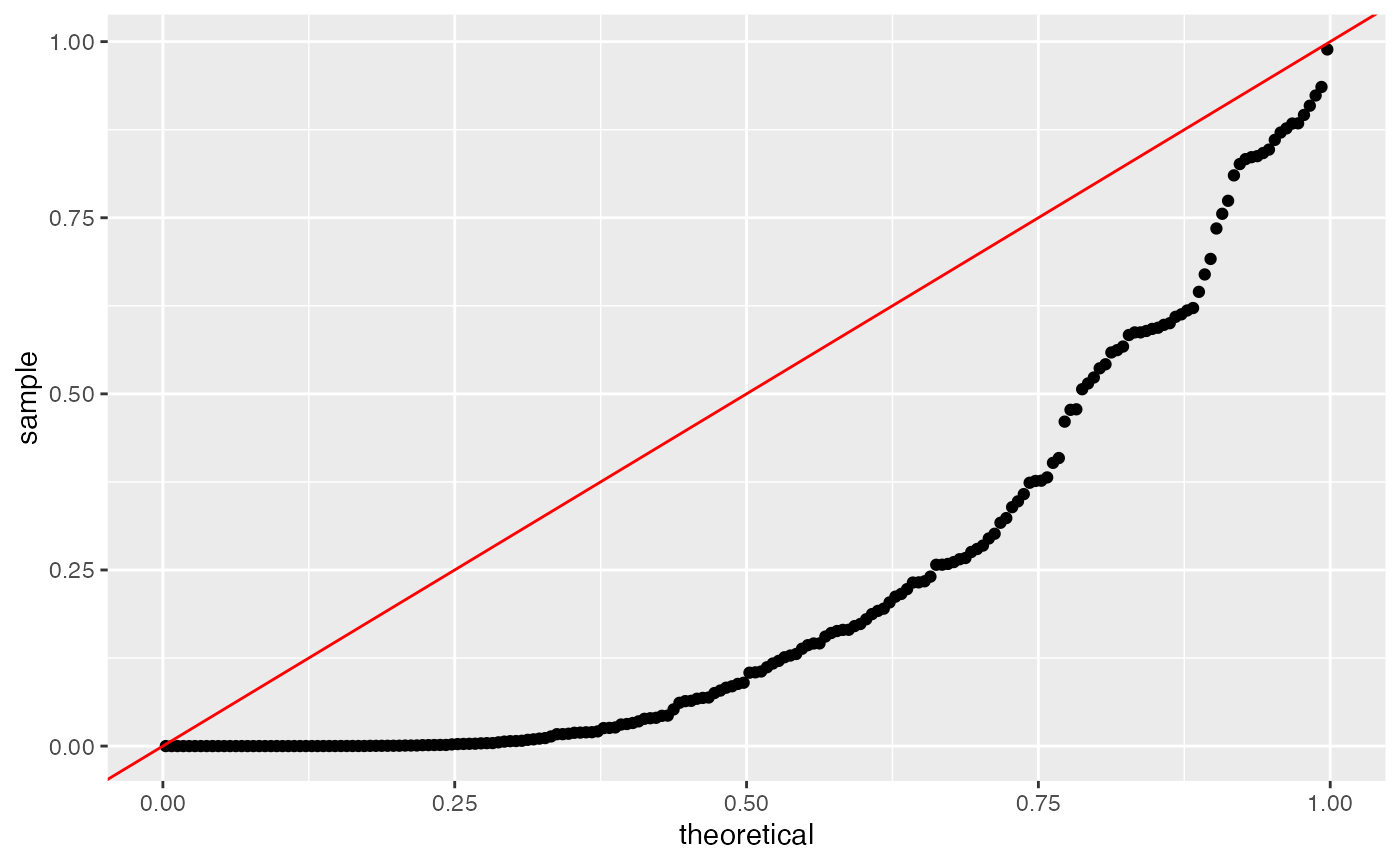

Poisson count splitting

We now address the issue using count splitting. In this section, we will (correctly) assume that the data follow a Poisson distribution. In the next section, we will consider the case where the data actually follow a negative binomial distribution.

The key steps are (1) running the countsplit function to get Xtrain and Xtest and then (2) clustering the data using Xtrain, and then fitting a GLM to test for association between those clusters and each column of Xtest. The countsplit function returns a list, which we call split here, which contains the training set and the test set.

Since we only want a single training set and a single test set, we will set folds=2 when calling countsplit. By default, this creates two identically distributed folds that each store half of the information in the dataset. We can change the amount of information allocated to the two folds by changing the epsilion parameter. When epsilon is very close to 0, the training matrix will be extremely sparse and the test matrix will look a lot like X. When epsilon is very close to 1, the training matrix will be nearly identical to X, but the test matrix will be extremely sparse. The default in the countsplit function is to set epsilon=c(0.5, 0.5). See our preprint for more information.

set.seed(2)
split <- countsplit(X, folds=2, epsilon=c(0.5,0.5))
Xtrain <- split[[1]]
Xtest <- split[[2]]

Like before, we will cluster using k-means with log-transformed data and we will fit Poisson GLMs for differential expression. Unlike before, we will run the clustering on Xtrain and use Xtest as the response in our GLMs.

clusters.train <- kmeans(log(Xtrain+1), centers=2)$cluster
results.countsplit <- t(apply(Xtest, 2, function(u) summary(glm(u~as.factor(clusters.train), family="poisson"))$coefficients[2,]))
head(results.countsplit)
##          Estimate Std. Error    z value   Pr(>|z|)
## [1,]  0.028171056 0.03988386  0.7063272 0.47998469
## [2,] -0.014424364 0.04075410 -0.3539365 0.72338648
## [3,]  0.007947168 0.04093763  0.1941287 0.84607511
## [4,]  0.024273036 0.04004166  0.6061945 0.54438561
## [5,] -0.067879740 0.04045377 -1.6779582 0.09335526
## [6,] -0.052881527 0.04004365 -1.3205971 0.18663572

We can see from the summary output that the p-values for the first 6 genes are much larger. When we make the same uniform QQ-plot as before, we see that the p-values obtained from count splitting are uniformly distributed. Since no genes are differentially expressed in our data, this means that count splitting controls the Type 1 error.

ggplot(data=NULL, aes(sample=results.countsplit[,4]))+geom_qq(distribution=stats::qunif)+geom_abline(col="red")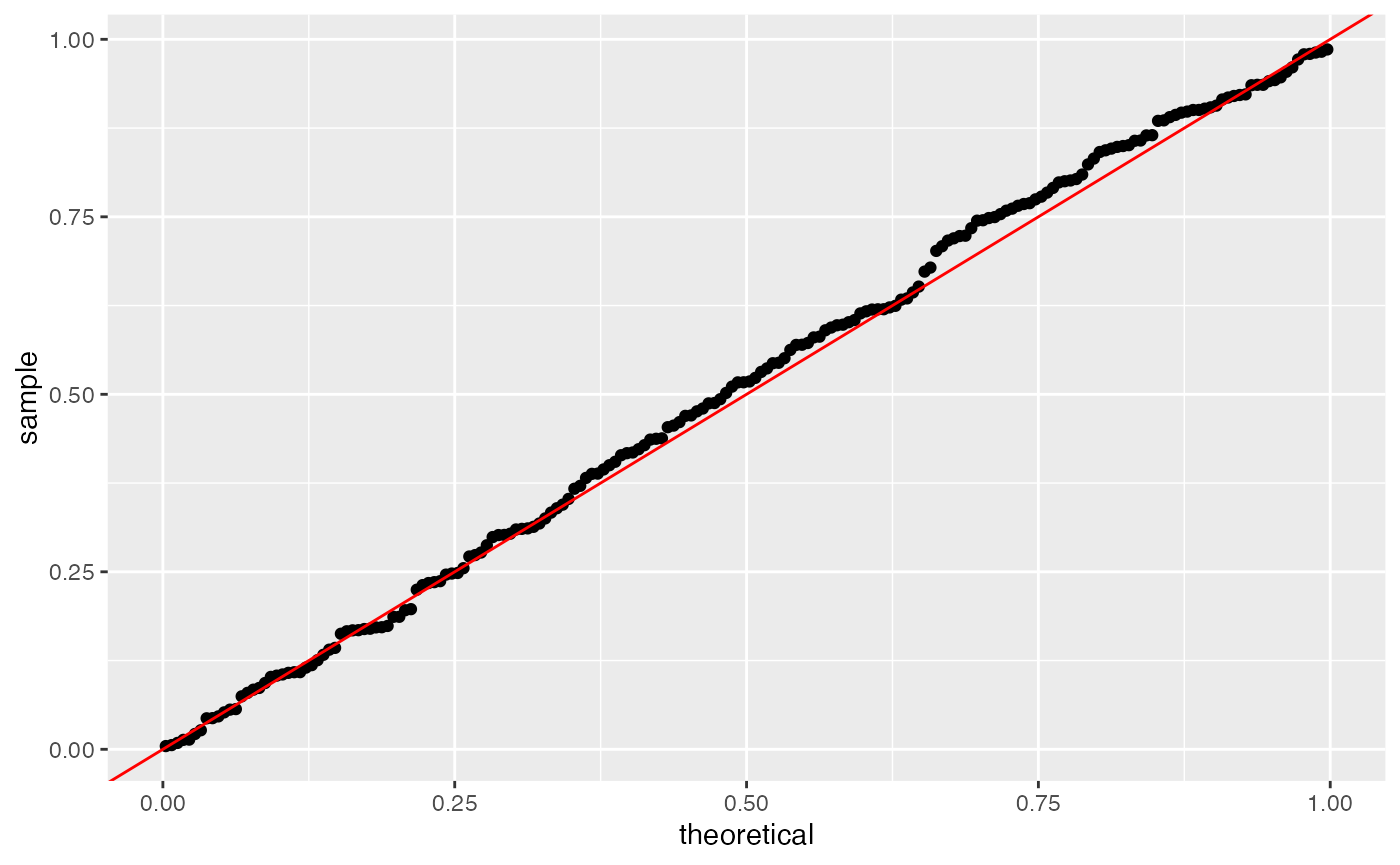

The crucial property that ensures that count splitting controls the Type 1 error in this setting is independence between Xtrain and Xtest. We can see that the columns of Xtrain are independent of the columns of Xtest in this data with no signal by looking at the sample correlations, which are centered around \(0\).

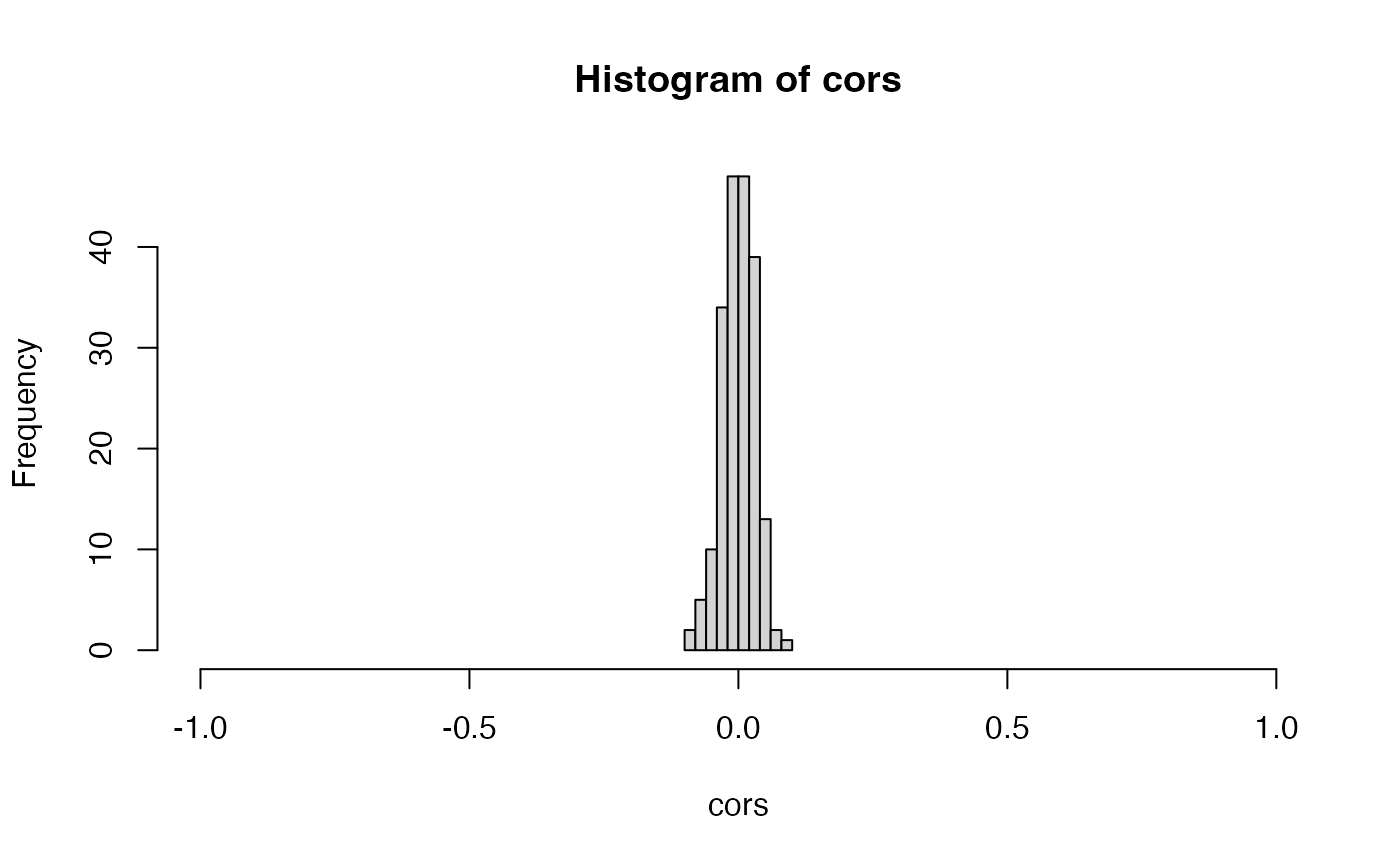cors <- sapply(1:p, function(u) cor(Xtrain[,u], Xtest[,u]))
hist(cors, xlim=c(-1,1))

In summary, count splitting controls the Type 1 error when there is no true signal in the data.

Simulated negative binomial data with no true signal

We now generate data with no true signal, but we generate the data from a negative binomial distribution. We use the mean + overdispersion parameterization of the negative binomial, in which the mean is given by mu and the variance is given by mu+mu^2/5.

set.seed(1)
n <- 1000
p <- 200
X <- matrix(rnbinom(n*p, mu=5, size=5), nrow=n)

## Sanity check on parameterization
mean(as.numeric(X))
## [1] 4.99826
var(as.numeric(X))
## [1] 9.966747
5+5^2/5
## [1] 10

Once again, in this part of the tutorial, we will cluster the data to estimate cell types and then test for differential expression. Since there are no true cell types and no truly differentially expressed genes in this data (all genes and all cells have mean \(5\)), a test of differential expression that controls the Type 1 error rate should give uniformly distributed p-values on this data. We will compare the naive method to three version of count splitting.

We first note that the naive method still fails to control the Type 1 error rate. We use a negative binomial GLM (as implemented in the MASS package, rather than a Poisson GLM, throughout this section).

clusters.full <- kmeans(log(X+1), centers=2)$cluster
results.naive <- t(apply(X, 2, function(u) summary(MASS::glm.nb(u~as.factor(clusters.full)))$coefficients[2,]))
ggplot(data=NULL, aes(sample=results.naive[,4]))+geom_qq(distribution=stats::qunif)+geom_abline(col="red")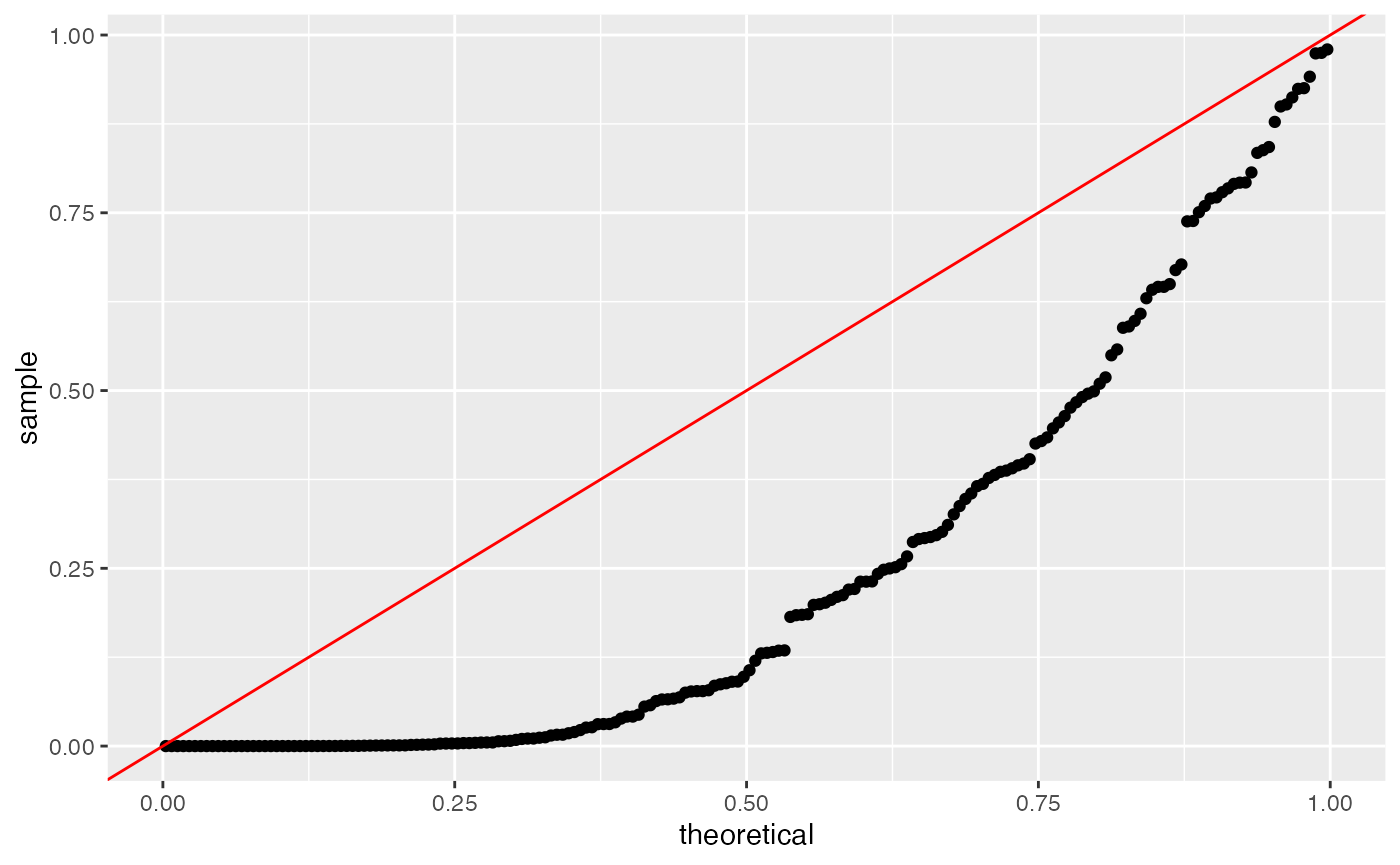

Unfortunately, we now also note that the default settings of count splitting will cause us to fail to control the Type 1 error rate. Note that we omit the arguments for folds and epsilon , because two equally sized folds is the default for count splitting.

set.seed(2)
split <- countsplit(X)
Xtrain <- split[[1]]
Xtest <- split[[2]]
clusters.train <- kmeans(log(Xtrain+1), centers=2)$cluster
results.countsplit <- t(apply(Xtest, 2, function(u) summary(MASS::glm.nb(u~as.factor(clusters.train)))$coefficients[2,]))
ggplot(data=NULL)+
  geom_qq(aes(sample=results.naive[,4], col="Naive method"),
  distribution=stats::qunif)+
  geom_qq(aes(sample=results.countsplit[,4], col="Poisson count splitting"), distribution=stats::qunif)+
  geom_abline(col="red")

By default, the countsplit function assumes that your data follow a Poisson distribution. Now that the data are not Poisson distributed, the default settings of countsplit fail to lead to independent training and test sets, as we can see by looking at the sample correlations between columns of Xtrain and columns of Xtest. These correlations will get worse as the amount of overdispersion in the negative binomial data increases.

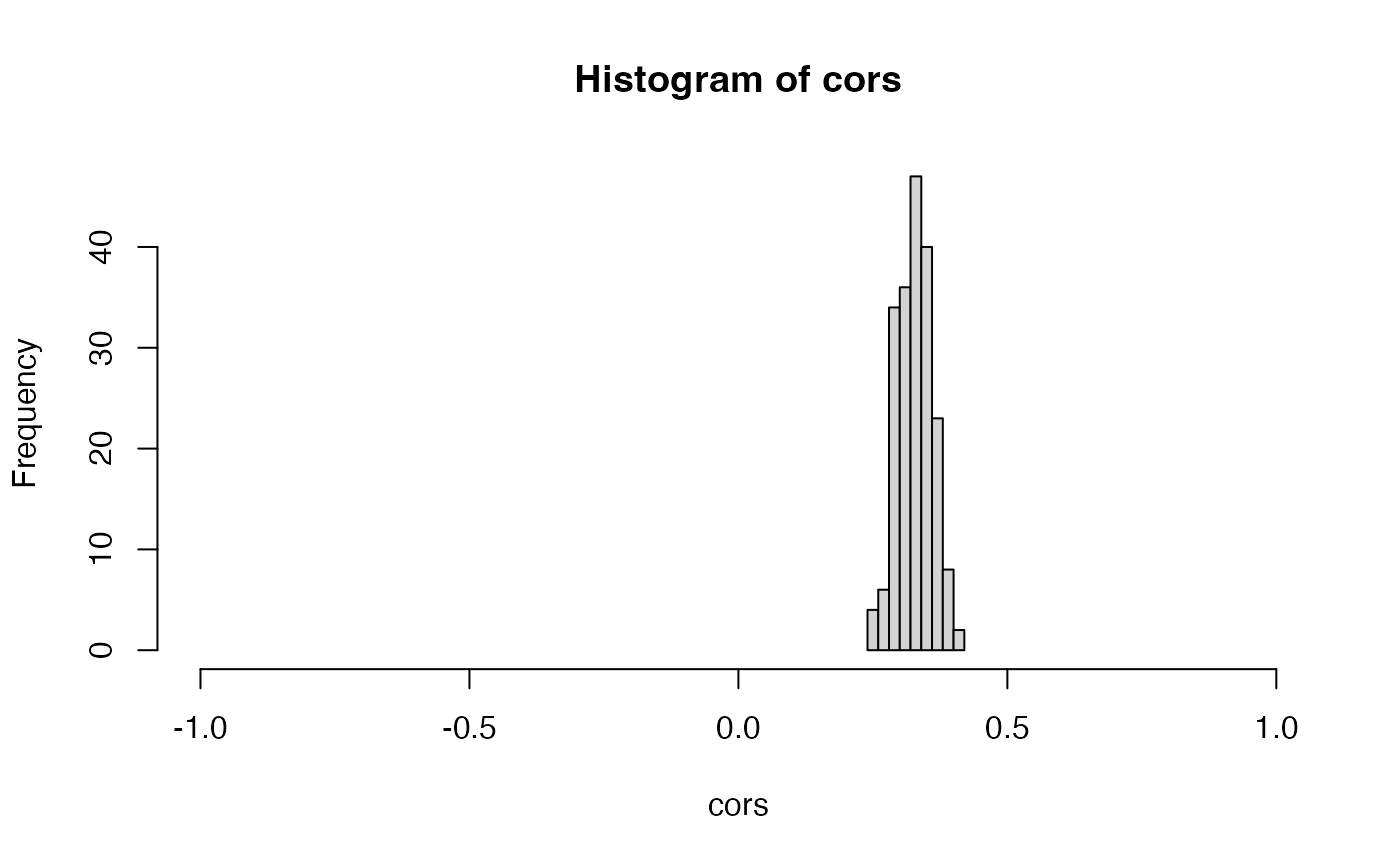
cors <- sapply(1:p, function(u) cor(Xtrain[,u], Xtest[,u]))
hist(cors, xlim=c(-1,1))

To deal with this, we must tell the countsplit function that our data are overdispersed. In this toy setting, we know the true value of the overdispersion parameter; it is \(5\) for all genes. So we can perform the ideal version of negative binomial count splitting where we plug in the value of \(5\) for every gene.

set.seed(2)
splitNB <- countsplit(X, overdisps=rep(5,p))
Xtrain <- splitNB[[1]]
Xtest <- splitNB[[2]]
clusters.train <- kmeans(log(Xtrain+1), centers=2)$cluster
results.countsplit.NB <- t(apply(Xtest, 2, function(u) summary(MASS::glm.nb(u~as.factor(clusters.train)))$coefficients[2,]))
ggplot(data=NULL)+
  geom_qq(aes(sample=results.naive[,4], col="Naive method"),
  distribution=stats::qunif)+
  geom_qq(aes(sample=results.countsplit[,4], col="Poisson count splitting"), distribution=stats::qunif)+
    geom_qq(aes(sample=results.countsplit.NB[,4], col="Ideal NB count splitting"), distribution=stats::qunif)+
  geom_abline(col="red")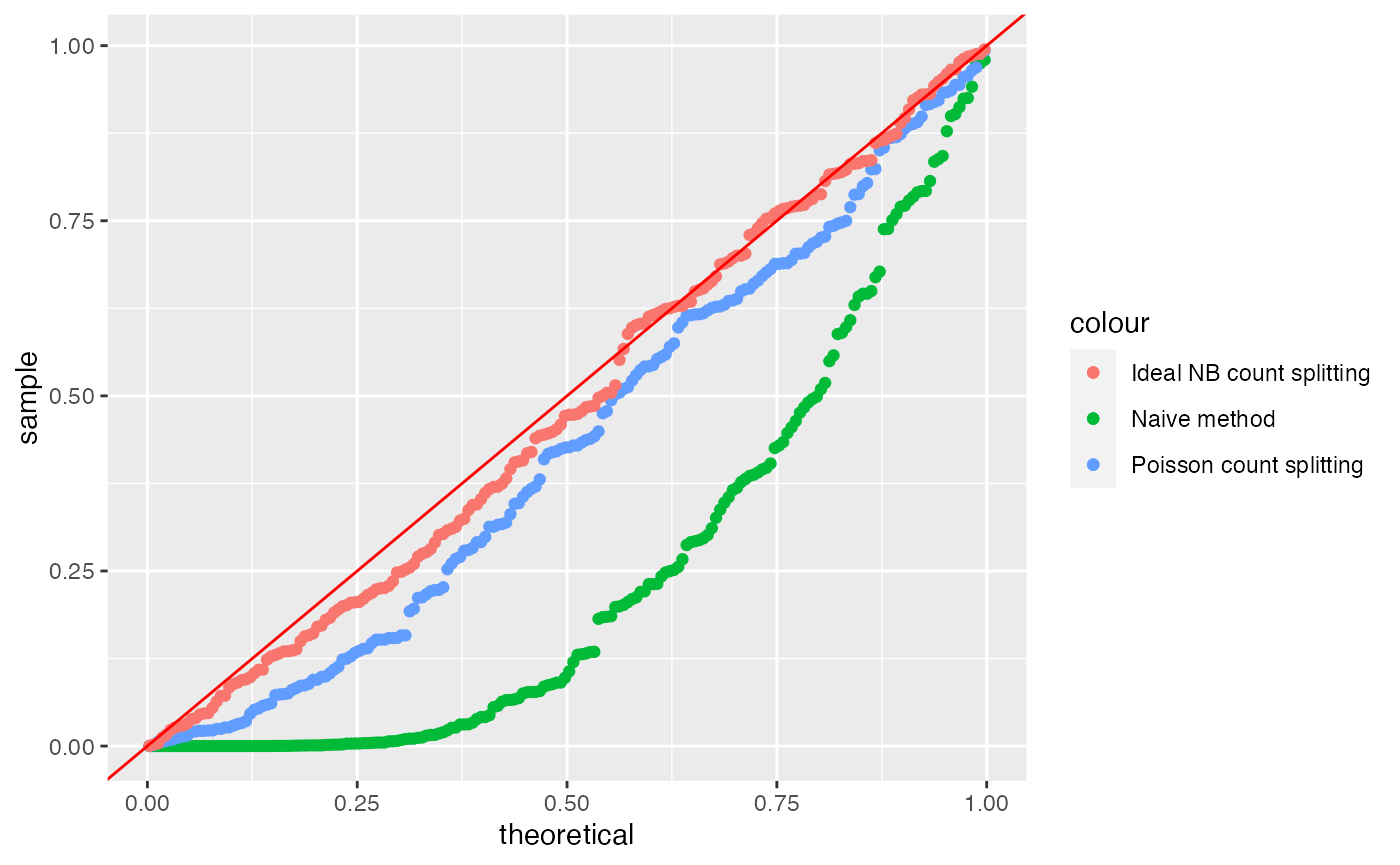

We see that we have recovered Type 1 error control. Unfortunately, in practice, we typically will not know the true value of the overdispersion parameter and will instead need to plug in a gene-specific estimate. A common way to estimate gene-specific overdispersion parameters is with the sctransform package in R. More specifically, if we call the vst() function from the sctransform package on the gene-by-cell matrix of counts (the transpose of \(X\), in this case), the estimated gene-specific overdispersion paramateters are stored in the first column of the model_pars section of the output.

rownames(X) <- 1:n
colnames(X) <- 1:p
overdisps.est <- sctransform::vst(t(X))$model_pars[,1]
## 
  |                                                                            
  |                                                                      |   0%
  |                                                                            
  |======================================================================| 100%
## 
  |                                                                            
  |                                                                      |   0%
  |                                                                            
  |======================================================================| 100%

By default, the vst() function does not necessarily return an estimated overdispersion for every single gene in the dataset. For example, it only returns an estimated overdispersion for genes that were expressed in at least 5 cells, and that were not found to be approximately Poisson distributed. The code below verifies that, in this case, we did in fact recieve an estimated overdispersion for all cells.

all.equal(names(overdisps.est), colnames(X))
## [1] TRUE

We can see that, in this case, the estimation of the overdispersion parameters went fairly well. All of the true overdispersion parameters are 5, and the estimated overdispersion parameters are all between \(4\) and \(6\).

hist(overdisps.est)

We are now prepared to apply negative binomial count splitting with these estimated parameters. We see that the performance is approximately as good as it was in the ideal version of negative binomial count splitting.

set.seed(2)
splitNB.est <- countsplit(X, overdisps=overdisps.est)
Xtrain.est <- splitNB.est[[1]]
Xtest.est <- splitNB.est[[2]]
clusters.train.est <- kmeans(log(Xtrain.est+1), centers=2)$cluster
results.countsplit.NB.est <- t(apply(Xtest.est, 2, function(u) summary(MASS::glm.nb(u~as.factor(clusters.train.est)))$coefficients[2,]))
ggplot(data=NULL)+
  geom_qq(aes(sample=results.naive[,4], col="Naive method"),
  distribution=stats::qunif)+
  geom_qq(aes(sample=results.countsplit[,4], col="Poisson count splitting"), distribution=stats::qunif)+
    geom_qq(aes(sample=results.countsplit.NB[,4], col="Ideal NB count splitting"), distribution=stats::qunif)+
    geom_qq(aes(sample=results.countsplit.NB.est[,4], col="Estimated NB count splitting"), distribution=stats::qunif)+
  geom_abline(col="red")

Simulated Poisson data with true signal

We now return to the Poisson setting, for simplicity. We demonstrate the performance of count splitting on a simple simulated dataset that contains two true clusters. We first randomly assign the cells to one of two true clusters. We then generate data such that \(X_{ij} \sim \mathrm{Poisson}(\Lambda_{ij})\). Genes 1-10 are differentially expressed– for \(j=1,\ldots,10\), \(\Lambda_{ij} = 5\) for cells in cluster \(0\) and \(\Lambda_{ij}=10\) for cells in cluster \(1\). Genes 11-200 are not differentially expressed (\(\Lambda_{ij}=5\) for all cells).

set.seed(1)
n <- 1000
p <- 200
clusters.true <- rbinom(n, size=1, prob=0.5)
Lambda <- matrix(5, nrow=n, ncol=p)
Lambda[clusters.true==1, 1:10] <- 10
X <-apply(Lambda,1:2,rpois,n=1)

We now count split the data and save Xtrain and Xtest for later use. Note that we don’t actually need to specify that we want two folds of data, as this is the default setting.

split <- countsplit(X)
Xtrain <- split[[1]]
Xtest <- split[[2]]

Effect of using Xtrain for cluster estimation.

First, let’s look at the effect of count splitting on our ability to estimate the true clusters. If we use all of our data X to estimate the clusters, we make only 5 errors.

clusters.full <- kmeans(log(X+1), centers=2)$cluster
table(clusters.true, clusters.full)
##              clusters.full
## clusters.true   1   2
##             0   5 515
##             1 480   0

If instead we use only Xtrain to estimate the clusters, we make a few additional errors, but we still come very close to estimating the true clusters.

clusters.train <- kmeans(log(Xtrain+1), centers=2)$cluster
table(clusters.true, clusters.train)
##              clusters.train
## clusters.true   1   2
##             0  17 503
##             1 468  12

The fact that cluster 0 in the true clustering maps to cluster 2 in the training set clustering is unimportant, but we will remember this later when we attempt to compare models.

Effect of using Xtest for inference

We now compare what happens when we regress \(X_j\) on the true clusters to what happens if we regress \(X_j^{\mathrm{test}}\) on the true clusters. We use the code below to fit a Poisson GLM of every gene on the true clusters; we save both the slope and the intercept. We are interested in the GLM slopes, as the GLM slopes are non-zero if the gene is differentially expressed across the clusters.

coeffs.X <- t(apply(X, 2, function(u) summary(glm(u~as.factor(clusters.true), family="poisson"))$coefficients[,1]))
coeffs.Xtest <- t(apply(Xtest, 2, function(u) summary(glm(u~as.factor(clusters.true), family="poisson"))$coefficients[,1]))

The plot below shows that the slopes resulting from X and the slopes resulting from Xtest tend to fall on the diagonal line y=x and so tend to be approximately equal to eachother. The intercepts, on the other hand, get shifted by log(0.5) when we use the Xtest rather than X. This is as we would expect (see Section 4.1 of our preprint).

differentially_expressed = as.factor(c(rep(1,10), rep(0,190)))
p1 <- ggplot(data=NULL, aes(x=coeffs.X[,1], y=coeffs.Xtest[,1], col=differentially_expressed))+
  geom_point()+
  geom_abline(intercept= log(0.5), slope=1, col="red")+
  geom_abline(intercept= 0, slope=1, col="red", lty=2)+
  coord_fixed()+xlim(0,2)+ylim(0,2)+
  xlab("Intercepts from X")+ ylab("Intercepts from Xtest")+
  ggtitle("Intercepts")+theme_bw()
p2 <- ggplot(data=NULL, aes(x=coeffs.X[,2], y=coeffs.Xtest[,2], col=differentially_expressed))+
  geom_point()+
  geom_abline(intercept=0, slope=1, col="red")+
  coord_fixed()+xlim(-0.15,1)+ylim(-0.15,1)+
  xlab("Slopes from X")+ ylab("Slopes from Xtest")+
  ggtitle("Slopes")+theme_bw()
p1 + p2 + plot_layout(guides="collect")

Overall comparison of count splitting to ideal method

Finally, we compare the overall slope and intercept estimates that we get from count splitting to what we would get in the ideal setting where we get to regress \(X_j\) on the true clusters. Note that coeffs.ideal is identical to coeffs.X from the previous section; we reproduce it here for convenience. Note also that we regress Xtest on as.factor(clusters.train==1), rather than as.factor(clusters.train), simply because we saw above that the “cluster 1” in the training set maps to the “cluster 1” in the true clustering, and this consistency will ensure that the coefficients from the two models have the same sign.

coeffs.ideal <- t(apply(X, 2, function(u) summary(glm(u~as.factor(clusters.true), family="poisson"))$coefficients[,1]))
coeffs.countsplit <- t(apply(Xtest, 2, function(u) summary(glm(u~as.factor(clusters.train==1), family="poisson"))$coefficients[,1]))
p1 <- ggplot(data=NULL, aes(x=coeffs.ideal[,1], y=coeffs.countsplit[,1], col=differentially_expressed))+
  geom_point()+
  geom_abline(intercept= log(0.5), slope=1, col="red")+
  geom_abline(intercept= 0, slope=1, col="red", lty=2)+
  coord_fixed()+xlim(0,2)+ylim(0,2)+
  xlab("Intercepts from ideal method")+ ylab("Intercepts from count splitting")+
  ggtitle("Intercepts")
p2 <- ggplot(data=NULL, aes(x=coeffs.ideal[,2], y=coeffs.countsplit[,2], col=differentially_expressed))+
  geom_point()+
  geom_abline(intercept=0, slope=1, col="red")+
  coord_fixed()+xlim(-0.15,1)+ylim(-0.15,1)+
  xlab("Slopes from ideal method")+ ylab("Slopes from count splitting")+
  ggtitle("Slopes")
p1 + p2 + plot_layout(guides="collect") & theme_bw()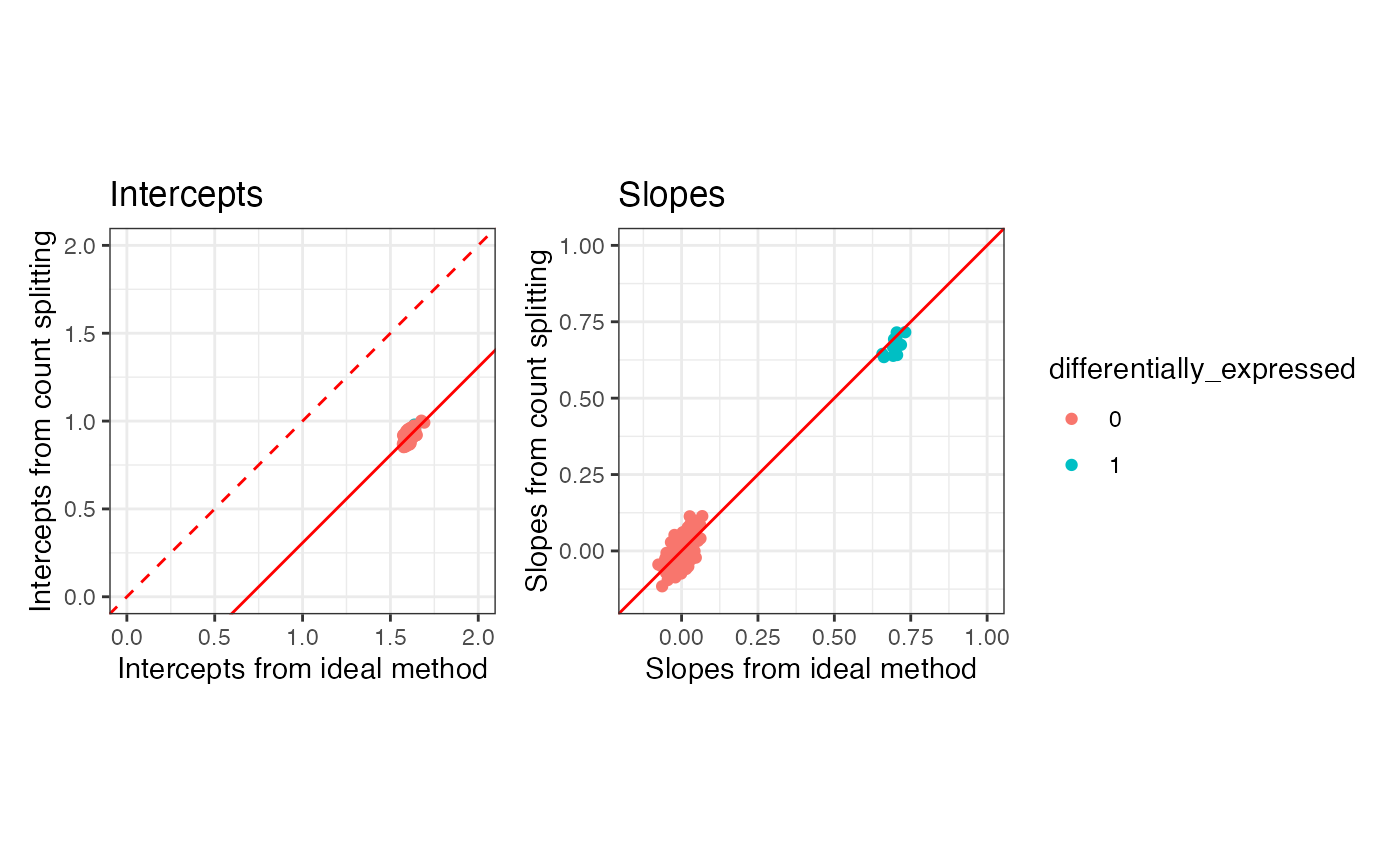

Overall, we see general agreement between the parameters estimated via countsplitting and those estimated via the ideal method. The slopes tend to be the same, whereas the intercepts are shifted by log(0.5), as expected based on our preprint. The slopes are the quantities that we care to do inference on, as they measure differential expression across clusters.